Theta Trend

When we begin trading Vertical spreads, Iron Condors, and Butterflies we learn that the trades are short vega.  In other words, they benefit from a decrease in implied volatility.  The opposite also generally holds true, meaning an increase in implied volatility should hurt the positions.  However, complex options positions are made up of individual options and each individual option has a unique Implied Volatility.  The change in the individual options is what ultimately makes up the position profit or loss and the changes in the prices and implied volatility of the individual options are the real drivers of the position.

The point of focusing on the individual options is that the implied volatility of the individual options can change in a way that benefits the position.  We’re going to discuss an open IWM Butterfly trade below.  The position is a short vega trade, meaning it benefits from a decrease in implied volatility, but we’ll discuss how an increase in implied volatility actually helped the position.

A brief note about option skew:

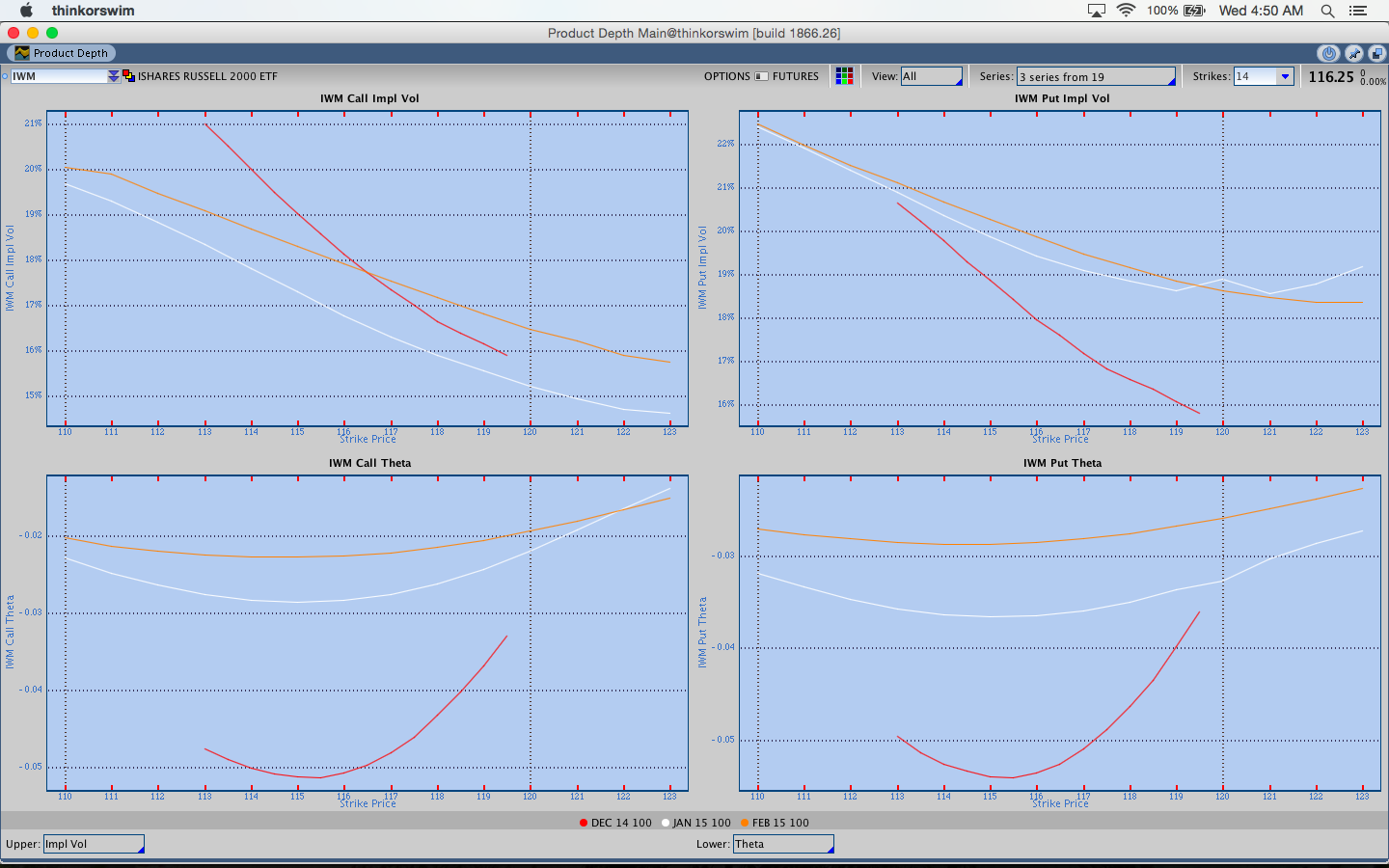
When we talk about the implied volatility of individual options along an option chain, we’re discussing skew.  We can visualize skew by plotting the implied volatility of individual options by strike and connecting those data points with a line.  In the Thinkorswim platform, we can see skew by going to the charts tab and then clicking product depth.  An image of IWM option skew from TOS is shown below.  Skew is static, but changes in skew over time present trading opportunities.

Getting into the IWM Option Butterfly Trade:

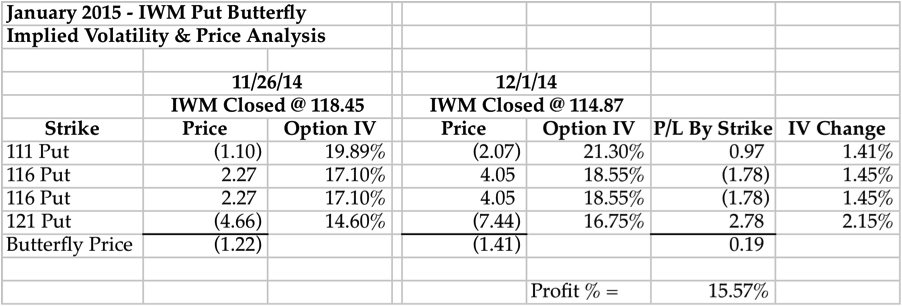
We’re going to walk through the first couple days of the January 2015 IWM Butterfly to show how an increase in implied volatility helped a short vega trade.  The table below lists the individual prices by strike and implied volatility for each option in the IWM Butterfly.  What we can see is that the trade was opened on November 26th for a 1.22 debit when IWM was trading a bit above 118.  A couple of days later, IWM fell below 115 and implied volatility spiked up (as we’d expect).  However, the spike in implied volatility actually helped the position.

If you take a look at the column labeled P/L by strike, you can see that despite losing money on the short 116 strikes in the middle of the Butterfly the trade was up money.  Essentially, the long option prices had increased in price more than the short options had decreased and that came from both a change in the price of IWM and an increase in implied volatility.  The implied volatility change column shows us that the biggest increase in implied volatility took place at the long 121 strike.  That change, combined with the increase at the 111 strike, more than offset the unfavorable change at the 116 strike.

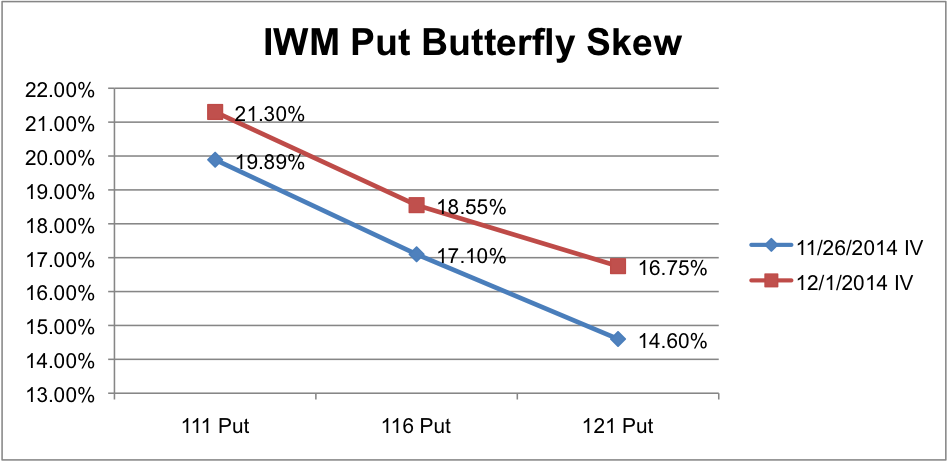
In the image below, we’re showing the IWM Option Skew for the Put Butterfly.  We can see that the biggest percentage change took place at the 121 strike.  The position ended up showing an open profit largely because the increase in implied volatility at the 111 and 121 strikes more than offset the loss at the 116 strike.

Great, so what’s the point?

The point of this discussion is that understanding the implied volatility of individual options matters and can be traded.  If we look at the changes in implied volatility above we’re seeing that an in the money option had a greater increase in implied volatility on a down move than an out of the money option.  Additionally, the further we went out of the money (111 vs 116) the less we saw implied volatility increase.  The Butterfly trade above was not taken based on IWM Put Skew, however, an opinion about the change in skew could be traded.  If we know that skew is steep and likely to flatted, we can construct a position to capitalize on that change.  Different positions could be traded if you expect skew to steepen.

The other take away from the IWM Butterfly is that an increase in implied volatility for a short vega trade does not always mean the trade will lose money.  In the IWM Options Butterfly above, the trade returned over 15% in less than a week largely because of an increase in implied volatility.

Thanks for reading and feel free to post questions in the comments below.